注意！这里的表述不一定精准，且不一定覆盖考点！

基本定义

字母表

由字母、数字、标点符号组成的集合

  • 乘积：A中取一个元素，B中取一个元素，两个连接起来后的集合
  • n次幂：长度为n的符号串构成的集合。n=0叫空串$\varepsilon $
  • 正闭包：各个正数次幂的并集，长度为正数的符号串构成的集合，用+号
  • 克林闭包：正闭包⋃\bigcup空串集合，长度为非负数的符号串构成的集合，用*号
串

由字母表中符号组成的有穷序列，包括空串。长度记作$\left | s \right | $，就是符号数

  • 连接运算：x和y的连接就是xy，空串是单位元
  • x=yz： y叫做x的前缀，z叫做x的后缀
  • 幂运算：s3=ssss^3=sss，0次就是空串
文法的形式化定义
  • 用四元组G表示，里面有VTV_T、Vn、P、S
  • 终结符Vt：不能再分割的基本符号
  • 非终结符Vn：可以再分割的中间符号，可以推导出其他东西
  • 终结符和非终结符没有公共元素，他们并起来叫文法符号
  • P叫产生式，就是一个串怎么变成另一个串的方法
  • S叫开始符号，就是推导开始的第一个串
推导和规约

推导就是拿P中的规则来去替换串中的某个元素，规约就是反操作

句型和句子
  • 句型就是由开始符号S推导出的一个串，里面可能有Vt、Vn和空串。
  • 句子是特殊的句型，里面只有终结符
  • 由文法G推出的所有句子叫文法G生成的语言，记作L(G)

看一下这个视频巩固基础概念：前导知识_哔哩哔哩_bilibili

根据文法G写出LG_哔哩哔哩_bilibili

文法的分类

  • 0型文法：a⟶ba\longrightarrow b，a中至少有一个非终结符

  • 1型文法（上下文有关文法）：∣a∣\left | a \right |<=∣b∣\left | b \right |，标准格式是α1Aα2→α1Bα2\alpha _{1} A\alpha _{2}\to \alpha _{1} B\alpha _{2}。就是说非终结符A，只有当它的上下文分别是a1,a2时，才能被替换为B。

  • 2型文法（上下文无关文法）：左部的a是非终结符即可

  • 3型文法（正则文法）：分为左线性文法和右线性文法

    比如左线性文法，右部要么是一个非终结符w，要么是终结符B+非终结符w，即A->Bw|w。右线性就是：A->wB|w

  • 1型文法建立在0型文法的基础上，2、3型文法同理。

上下文无关文法的分析树

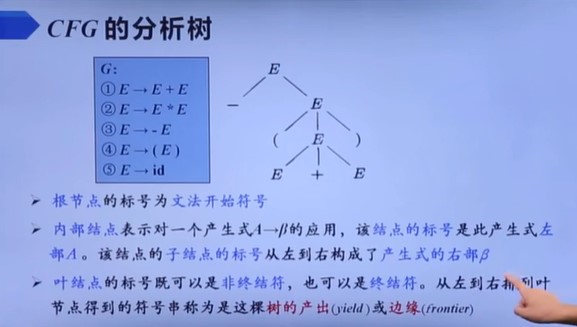
短语

选定一个根节点后，这个根节点延申出的子树的边缘。比如

  • -（E+E)
  • (E+E)
  • E+E
直接短语

就是这棵子树高度是2，只有父子节点，然后它的边缘叫直接短语，就是这里的E+E。直接短语肯定是某个产生式P的右部，反之不一定。

句柄

在分析树最左边的直接短语

素短语和最左素短语

素短语，是指至少含有一个终结符的短语，并且其内部不再含有素短语。
最左素短语是句型中最左边的素短语。

短语，直接短语，素短语与最左素短语（语法树求法）-CSDN博客

编译原理－求短语，直接短语，句柄，素短语，最左素短语_哔哩哔哩_bilibili

文法二义性

这个文法能够为一个句子生成多棵分析树

怎么判断和怎么修正二义性：消除文法二义性总结_哔哩哔哩_bilibili

必考题型：

分析句型构造语法树_哔哩哔哩_bilibili

根据语法树求短语，直接短语，句柄_哔哩哔哩_bilibili

这里还会有给你一个语言，要你写出语法的题型：由语言构造文法-CSDN博客

词法分析

正则表达式

正则表达式和正则文法是等价的，一个存在另一个也存在。

这个要会转换

正规式转正规文法_哔哩哔哩_bilibili

正规文法转正规式_哔哩哔哩_bilibili

正则定义

这个好像没什么用?^?

有穷自动机定义
转换图

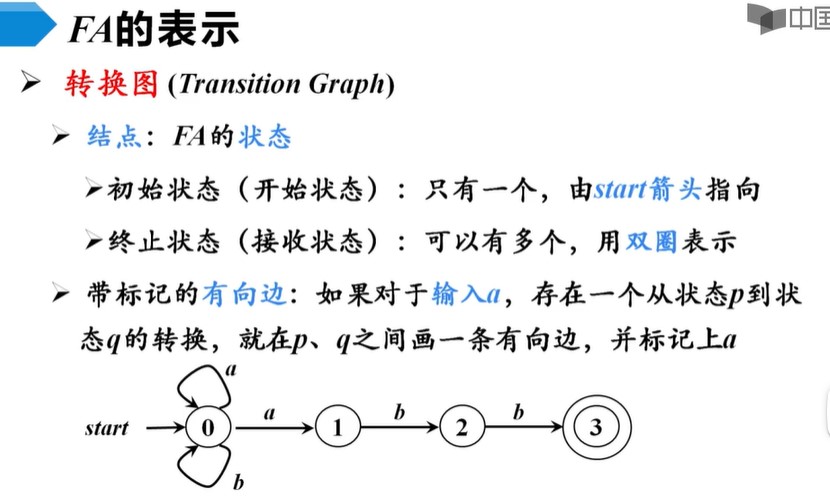
串能够被FA接收

给一个串s，一个一个字母输入转换图中，最后存在到达终止状态的一种可能，就叫可被接收。

比如s=abbaabb，前4个abba先在状态0上旋转，后三个abb正好能到状态3（终止状态），只要有这种可能就说明串可被接收。

一个自动机M可以接收的所有串的集合叫FA接收的语言，记作L(M)。对上面这个例子来说，L(M)就是{a,b}*+abb

最长字串匹配原则

就是有穷自动机的运行准则。自动机会永远选择最长的前缀进行匹配直到匹配不上为止。

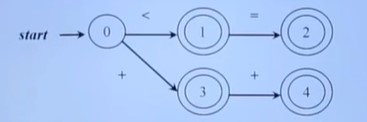
比如上图这种，如果输入是<=，那会到2这个终态；输入是++，会到4这个状态。

有穷自动机分类
确定有穷自动机DFA

举个栗子看下图

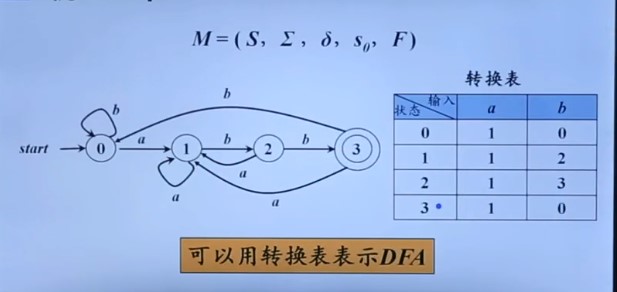
上图中

  • 有穷状态集S就是0、1、2、3四种状态
  • 输入字母表Σ\Sigma就是a、b
  • 转换函数就是上图中的转换表
  • 开始状态s0就是0，接收状态F就是3
非确定有穷自动机NFA

NFA和DFA的唯一区别就在于：从某个状态出发，沿着某个输入，可以有多个目标结果，可以看下图的栗子。

带空串的NFA

而且空串也可以作为转换函数的输入，看下面的图。

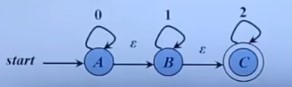
这个的意思是A不需要接收什么信号就可以到B，B到C同理。但是并不说明A和B是相同的状态，因为A可以接收0输入，而一旦到了B，就只能接收1输入而无法接收0输入了。这个图的正则表达式是：0∗1∗20^*1^*2

实际上，DFA、NFA和带空串的NFA之间是可以互相转换的，后面就开始讲这个

从正则表达式构造DFA

这个分两步完成，先从正则表达式构造NFA，再把NFA转换成DFA

正则表达式构造NFA：正归式转NFA_哔哩哔哩_bilibili

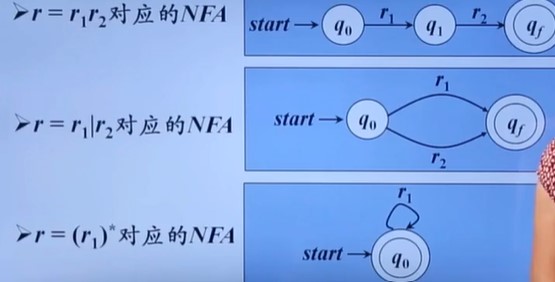
NFA转换成DFA：这个也叫确定化。这个有点抽象，直接看例子去吧。

3-6从NFA到DFA的转换_哔哩哔哩_bilibili

DFA（NFA确定化）以及DFA最小化_哔哩哔哩_bilibili

DFA化简：最小化

编译原理正规表达式转NFA到DFA再化简_哔哩哔哩_bilibili看这个视频直接一步到位

语法分析

自顶向下分析

从分析树根节点向叶节点构造，就是从开始符号S推具体串的

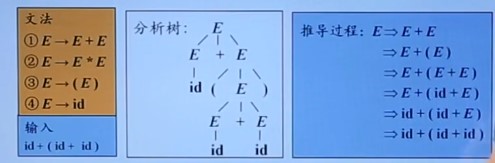
这种情况下替换非终结符要考虑两方面：替换哪个E、用哪条文法准则来替换

先讲替换哪个E怎么确定：最左推导和最右推导

最左/右推导

最左：把最左边的非终结符替换到只剩终结符为止

这个东西从上到下叫最左推导，从下到上叫最右规约。

经过最左推导推出的叫最左句型

最右：和上面那个反过来

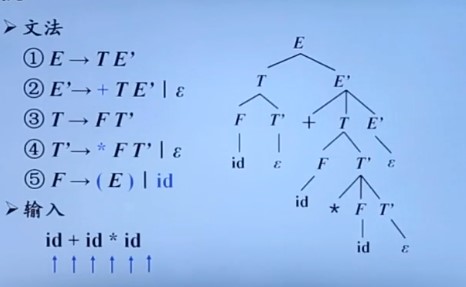
把最左规约称为规范规约（因为自底向上分析用最左规约），最右推导称为规范推导

在自顶向下分析用最左推导，下面图片是一个栗子：

递归下降分析程序

左递归

而当一个非终结符的多个候选式存在共同前缀时，会发生回溯现象，例如S->aAd|aBe，当输入字符串为a时，S需要尝试两种可能情况；例如文法E->E+T|E-T|T，当输入字符串为id时，文法的三个选择中均没有id项，要尝试多种情况，甚至陷入无限循环。

形如A->Aa的文法叫直接左递归，经过多步推导产生的左递归叫间接左递归；发生这种情况的文法叫左递归文法，左递归文法会使递归下降分析程序陷入无限循环。

如何消除左递归？

消除文法左公共因子和左递归_哔哩哔哩_bilibili

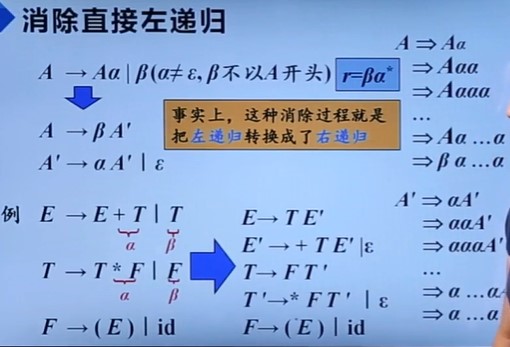
LL(1)文法

LL(1)文法的判别_哔哩哔哩_bilibili

求FIRST集，FOLLOW集，SELECT集_哔哩哔哩_bilibili

构造LL(1)预测分析表_哔哩哔哩_bilibili

必考题型

  • 给一个句型和语法，画语法树，然后写短语、直接短语、句柄、素短语、最左素短语。
  • 给一些条件，写正规表达式，然后把正规表达式变成正规文法，然后要会正规式转NFA、NFA转DFA和DFA的最小化。
  • 给一个语法，会算FIRST集、FOLLOW集和SELECT集，要会画构造分析表，并且能够判断这个文法是不是LL1型文法，最后要写它的递归下降分析程序。

可能题型

  • 给一个语言或者一些条件，写出它的文法。
  • 给一个句子和文法，让你写最左推导和最右推导
  • 判断某个文法是否有二义性，以及如何消除二义性
  • 给正规文法让你写正规式
  • 证明两个正规式等价：即说明两者的最小DFA一致
  • 拿到正规式，写左线性文法和右线性文法

图片

必考题2

正规式转正规文法：

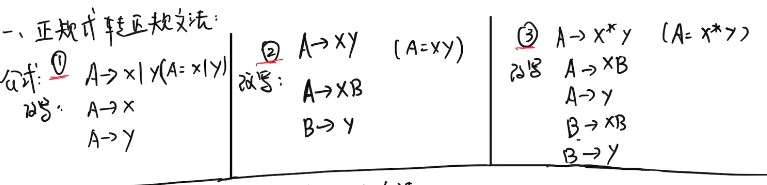
正规文法转正规式：

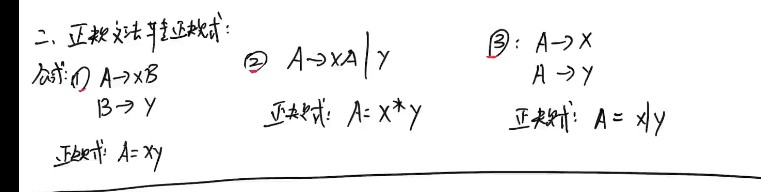
可能题6

必考题3

写某个串的分析过程：